


Qu'est ce qu'un dôme géodésique ?
| Définition Mathcurve
: On désigne par dômes géodésiques les polyèdres inscriptibles à faces
triangulaires et sommets de degrés 5 ou 6, ainsi que les polyèdres
duaux de ces derniers (autrement dit les polyèdres circonscriptibles à
sommets de degré 3 et à faces hexagonales ou pentagonales) Voici une méthode de construction d'un dôme géodésique type (a,b) à partir d'un icosaèdre. Pour chaque face de l'icosaèdre : 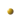 On part du sommet A du triangle et on trace les points P0, P1, ...Pa+b partageant un côté [AB] en a+b segments de même longueur On part du sommet A du triangle et on trace les points P0, P1, ...Pa+b partageant un côté [AB] en a+b segments de même longueur 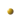 On trace le segment [CPa] On trace le segment [CPa]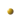 On trace alors la famille de droites parallèles à (CPa) et passant par les points P0, P1, ...Pa+b On trace alors la famille de droites parallèles à (CPa) et passant par les points P0, P1, ...Pa+b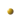 On recommence le même travail avec les autres côtés. On recommence le même travail avec les autres côtés.  On obtient alors des triangles équilatéraux (certains incomplets) dont nous allons projeter les sommets sur la sphère circonscrite. On obtient alors des triangles équilatéraux (certains incomplets) dont nous allons projeter les sommets sur la sphère circonscrite. On remarque au passage que le rapport des aires du petit triangle équilatéral par rapport à celui de départ vaut D=a²+ab+b² que l'on appelle la densité du dôme. On remarque au passage que le rapport des aires du petit triangle équilatéral par rapport à celui de départ vaut D=a²+ab+b² que l'on appelle la densité du dôme.On obtient alors un dôme comportant 20D faces, 30D arêtes et 10D+2 sommets : 12 de degré 5 et 10(D-1) de degré 6. |
|